经典非对称加密算法:RSA
单向函数(One-way Function)
对于每一个输入,函数值都容易计算(多项式时间);但是对于一个随机的函数值,算出其对应的输入却比较困难(无法在多项式时间内使用确定性图灵机计算)。
最简单的单向函数是取模运算:m mod n = a
例如 11 mod 2 = 1 ,根据输入的数据11很容易知道输出结果是1,但是根据输出结果1无法知道输入数据是什么
m 作为原文,n 作为公开的密钥,a 作为加密后的密文 —— 即使我们拿到了密钥也无法解密,因为这是不可逆的
密码学的新方向 —— 单向陷门函数(One-way Trapdoor Function)
单项陷门函数是有一个陷门的一类特殊单向函数。单项陷门函数包含两个明显特征:一是单向性,二是存在陷门。
单向函数存在 bug(陷门)吗?即可以实现单向函数的逆推。如果存在一种单向算法存在陷门,那么可以将这个算法称为单向陷门函数(One-way Trapdoor Function)
在1976年 W. Diffie 和 M. Hellman 提出了这样的美好设想:
信息的接收者提前生成两个密钥,将一个单项陷门函数作为加密密钥公开发布(即公钥),信息的发送者使用公钥加密信息,信息的接收者自己保留的解密密钥(即私钥)就是这个单项陷门函数的陷门,接收者可以使用私钥解密加密后的密文
密文可以被截获,但窃密者不持有私钥,无法解密密文。私钥永远在接收者手里,这样就没有了发送密钥被截获的风险
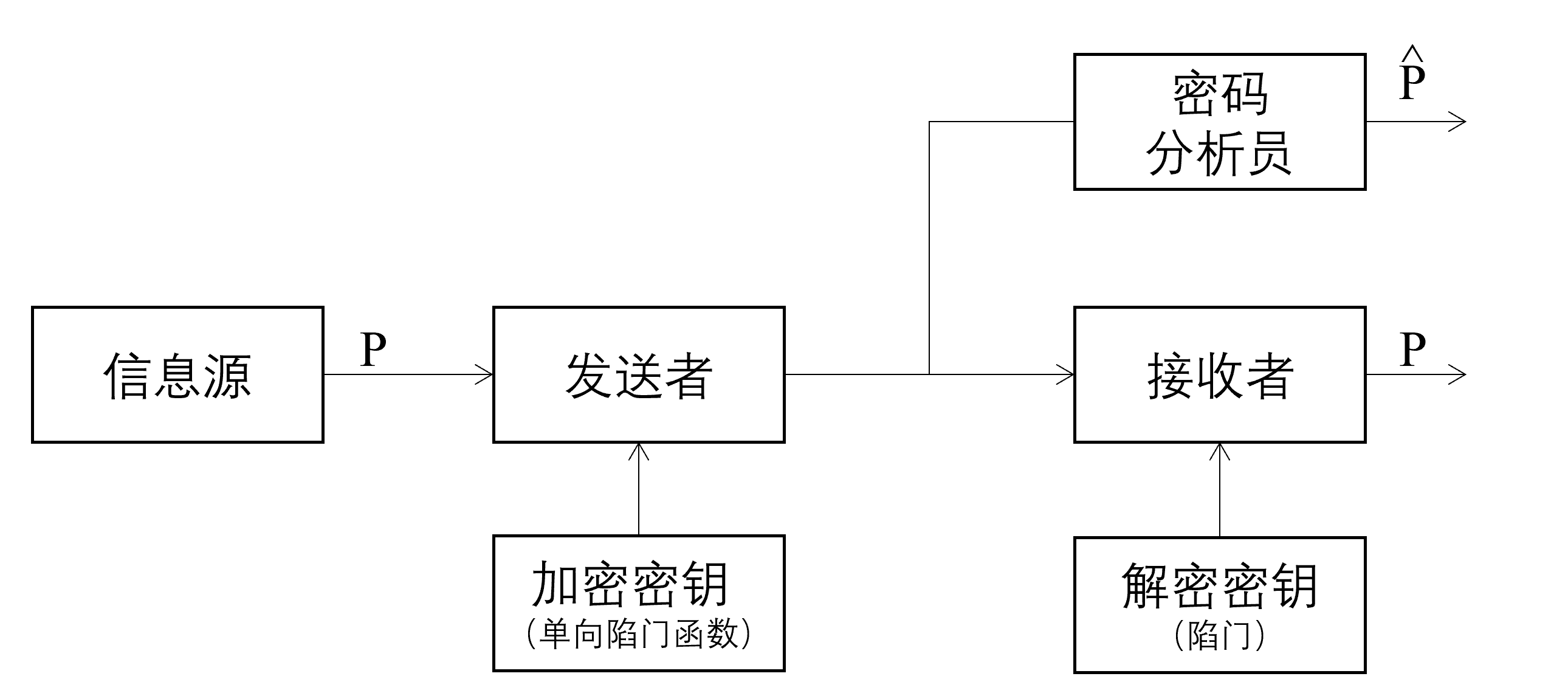
自此,密码学有了新的方向 —— 公钥密码,加解密的不对称也被称为非对称密码
之所以在前文说这是 Diffie 和 Hellman 的美好设想,是因为 Diffie 和 Hellman 并没有找到合适的单向陷门函数……
RSA加密算法
R. L. Rivest、A. Shamir 和 L. Adleman 三人在 1978 年发表了题为 A Method for Obtaining Digital Signatures and Public-key Cryptosystems 的论文,在文中首次系统地提出了一种以三人姓氏命名的公钥加密算法——RSA 算法
在 RSA 体制中,对于给定的乘方取模运算:
其中 $m$ 为明文,$c$ 为密文,$(e,n)$ 为加密所用的公钥。
解密时希望存在某个指数 $d$,使得对密文 $c$ 执行以下“逆运算”,能还原出明文 $m$ :
我们可以把私钥指数 $d$ 看作这一乘方取模运算的“陷门”(trapdoor),因为一旦掌握 $d$,就可以有效地对 $c = m^e \bmod n$ 进行逆运算,恢复出明文 $m$。
一、RSA 的基本形式
- 公钥:$(e,n)$
- 私钥:$(d,n)$
将加密公式代入解密公式,有:
即
若能保证对所有与 $n$ 互质的 $m$ 都有
就可以实现正确解密。根据欧拉定理,若 $\gcd(m,n)=1$,则有
由于
对等式两边同时乘方任意整数次 $k$,则有
两边再同乘一个 $m$,有
因此,只要令
即存在整数 $k$ 使
就能保证
解密过程即按预期恢复出明文。
二、欧拉函数 $\varphi(n)$ 及其在 RSA 中的计算
欧拉函数 $\varphi(n)$ 定义为:不大于 $n$ 且与 $n$ 互质的正整数的个数。
在 RSA 算法中通常取 $n = pq$,其中 $p,q$ 为两个不同的大素数。
由欧拉函数乘法性结论可知:当 $p,q$ 为互质素数时,有
证明如下:
设 $n = pq$,其中 $p,q$ 互质且为素数。考虑集合 ${1,2,\dots,n}$ 中与 $n$ 不互质的整数。
- 所有被 $p$ 整除的数为 ${p,2p,\dots,(q-1)p,qp}$,共有 $q$ 个;
- 所有被 $q$ 整除的数为 ${q,2q,\dots,(p-1)q,pq}$,共有 $p$ 个。
其中 $pq$ 被 $p$ 和 $q$ 同时整除,在上面两类中被重复计算一次,因此与 $n$ 不互质的数共有 $p + q - 1$ 个。
从 ${1,2,\dots,n}$ 中去掉这些与 $n$ 不互质的数,则与 $n$ 互质的数的个数为:
三、欧拉定理及其证明
欧拉定理:若 $\gcd(c,n)=1$,则
证明如下:
设所有小于等于 $n$ 且与 $n$ 互质的整数为
取任意 $c$,满足 $\gcd(c,n)=1$。对每个 $a_i$,考虑乘积
由于 $c$ 与 $n$ 互质,乘法在模 $n$ 的剩余类中是一个双射映射,所以集合
只是 ${a1,a_2,\dots,a{\varphi(n)}}$ 的一个重新排列。
因此有:
展开左边得到:
由于 $\prod_{k=1}^{\varphi(n)} a_k$ 与 $n$ 互质,可以在模 $n$ 意义下约去该乘积,最终得到:
得证欧拉定理。
四、解密指数 $d$ 的构造与存在性条件
由欧拉定理可知,对任意与 $n$ 互质的 $m$ 有
因此对任意整数 $k$
进一步得到
若令
则
即解密公式成立。此时有:
要使 $d$ 为整数,必须保证存在整数解 $d$,即
等价于
也就是说,公钥指数 $e$ 必须与 $\varphi(n)$ 互质。
五、数值示例与 $d$ 的选择
例如,设 $n = 34$。因为
取 $e = 15$,则 $\gcd(15,16)=1$,存在整数 $d$ 使得
由于 $15 \equiv -1 \pmod{16}$,上式可写为
因此最小正整数解为 $d = 15$
从 $ed = k\varphi(n)+1$ 角度来看,有
取 $k = 14$ 时
若取 $k = 29$,则
同样是一个整数解,并满足 $d \equiv 15 \pmod{16}$。在实际 RSA 中,我们通常选取最小的正整数解作为私钥指数 $d$。
快速求解这一类同余方程 $ed \equiv 1 \pmod{\varphi(n)}$ 的标准方法是扩展欧几里得算法,它能高效地给出 $e$ 在模 $\varphi(n)$ 意义下的逆元 $d$。
六、RSA 实际运用与安全性
接收者生成密钥:
选取两个足够大的素数 $p$ 和 $q$,计算 $n = pq$;
计算 $\varphi(n) = (p-1)(q-1)$;
选取一个与 $\varphi(n)$ 互质的整数 $e$ 作为公钥指数;
利用扩展欧几里得算法求解
得到私钥指数 $d$。
发布公钥:
接收者将 $(e,n)$ 公开作为公钥,$(d,n)$ 保密作为私钥。发送者加密:
发送者要传输明文 $m$(通常要求 $0 \le m < n$ 且 $\gcd(m,n)=1$),使用公钥进行加密:接收者解密:
接收者收到密文 $c$ 后,用私钥解密:从而恢复原始明文 $m$。
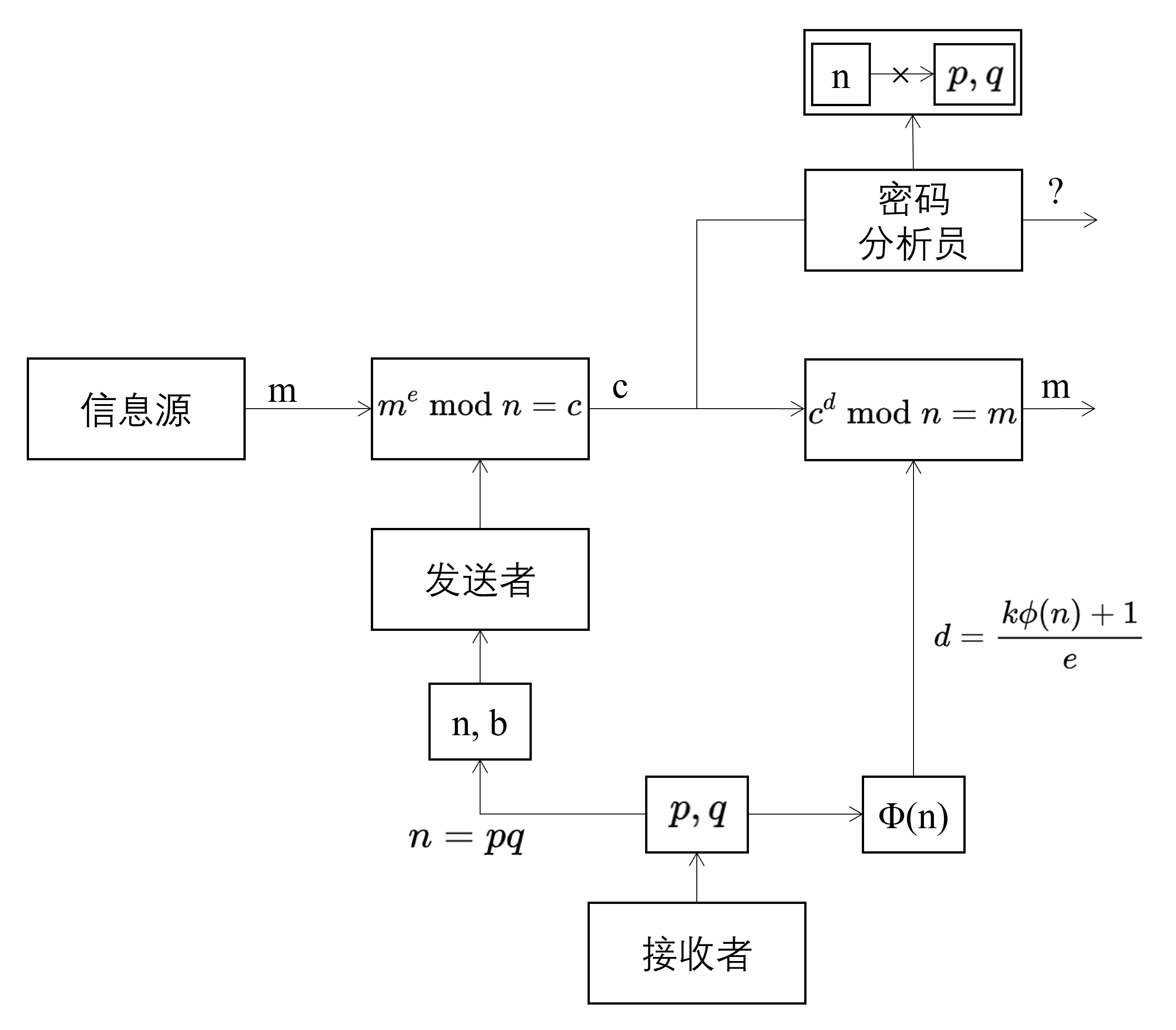
RSA 的安全性主要基于如下事实:
若已知 $p,q$,则可以轻易计算 $\varphi(n)$,进而由 $e$ 计算出 $d$;
但对于足够大的 $n$,如
1
n = 22112825529529666435281085255026230927612089502470015394413748319128822941402001986512729726569746599085900330031400051170742204560859276357953757185954298838958709229238491006703034124620545784566413664540684214361293017694020846391065875914794251435144458199
将 $n$ 分解为 $p$ 与 $q$ 在计算上极其困难。
因此,虽然公钥 $(e,n)$ 是公开的,但攻击者在没有办法分解出 $n$ 的前提下,难以求得 $\varphi(n)$,也就难以求出私钥 $d$,从而无法从截获的密文中恢复明文。
Reference
[1] Rose-Hulman Scholar . https://scholar.rose-hulman.edu/cgi/viewcontent.cgi?article=1081&context=rhumj